Partial sums with unique input elements, for an alphabet of k elements, the time it takes to find a solution is at most 2^k, regardless of the size of the input. To flip that around, partial sums is solvable in O(n^k) where n is the size of the input and k is the size of the alphabet. Not that this does you any good, of course.
Notation duly abused.
art with code
2017-08-24
More on P & NP & partial sums
Another hack search problem solvable in polynomial time by a non-deterministic machine but not by a deterministic one. But it's not a proper problem. Suppose you have an infinitely large RAM of random numbers (yeah, this starts out real well). The problem is to find if an n-bit number exists in the first 2^n bits of the RAM.
As usual, the deterministic machine has to scan the RAM to find the number, taking around 2^n steps. And as usual, the non-deterministic machine just guesses the n bits of the address in n steps and passes it to checkSolution, which jumps to the address and confirms the solution. Now, this is not an NP-complete problem in this formulation, since the contents of the RAM are not specified, so there's no mapping from other NP-complete problems to this.
Jeez, random numbers.
Given the lottery numbers for this week's lottery, compute the lottery numbers for next week's lottery. Non-deterministic machine: sure thing, done, bam. Deterministic machine: this might take a while (btw, is simulating the universe a O(n^k)-problem?) Check solution by checking bank account.
Unique inputs partial sums then. First off, sort the inputs, and treat them as a binary number where 0 is "not in solution" and 1 is "in solution".
If all the numbers in the input are such that the sum of all smaller inputs is smaller than the number, you can find the solution in linear time. For (i = input.length-1 to 0) { if (input[i] <= target) { target_bits[i] = 1; target -= input[i]; } else { target_bits[i] = 0; }}
You can prune the search space by finding a suffix that's larger than the target and by finding a prefix that's smaller than the target. Now you know that there must be at least one 0-bit in the larger suffix and at least one 1-bit in the suffix of the smaller prefix.
The time complexity of partial sums is always smaller than 2^n. For a one-bit alphabet, the time complexity is O(n). For a two-bit alphabet, the max time complexity is 2^(n/2) as you need to add two bits to the input to increment the number of elements in the input. So for an 8-bit alphabet, the max complexity would be 2^(n/8).
The complexity of partial sums approaches easy as the number of input elements approaches the size of the input alphabet. After reaching the size of the input alphabet, a solution exists if (2^a + 1) * (2^a / 2) <= target (as in, if the sum of the input alphabet is greater than or equal to target. And if the input alphabet is a dense enumeration up from 1.) You can find the solution in O(n log n): sort input, start iterating from largest & deduct from the target until the current number is larger than the target. Then jump to input[target] to get the last number. You can also do this in O(n) by first figuring out what numbers you need and then collecting them from the input with if (required_numbers[input[i]]) pick(input[i]), required_numbers can be an array of size n.
Once you reach the saturated alphabet state, you need to increase the size of the alphabet to gain complexity. So you might go from an 8-bit alphabet with a 256 element input to a 9-bit alphabet with a 256 element input (jumping from 2048 to 2304 bits in the process, hopefully boosting the complexity from O(256)-ish to O(2^256)-ish).
Thankfully, as you increase the alphabet size by a bit, your input size goes up linearly, but the saturation point of your alphabet doubles. At a fixed input size in bits, increasing the alphabet size can decrease the complexity of the problem, for each bit increase you can go from 2^(n/k) -> 2^(n/(k+1)). Likewise, by decreasing the alphabet size, you can increase the complexity of the problem. Increasing the number of elements in the input can increase the complexity of the problem, while decreasing the number of elements can decrease the complexity. The "can" is because it depends. If you're close to saturation, increasing the number of elements can nudge the problem from O(n^2) to O(n), ditto for decreasing the alphabet size. Whereas increasing the alphabet size at saturation can turn your O(n) problem into an O(2^n) problem.
As your alphabet gets larger, the discontinuities stop being so important. Anyhow, for a given partial sums input size in bits, the problem is O(n) for alphabet sizes <= log2(n). The difficulty of the problem scales with the target as well. For targets smaller than the smallest input element and for targets greater than the greatest input element, it takes O(n) time.
Tricks, hmm, the number of search-enhancing tricks you can use depends on the input. I guess the number of tricks is somehow related to the number of bits in the input and grows the program size too. The ultimate trick machine knows all the answers based on the input and has to do zero extra computation (yeah, this is the array of answers), but it's huge in size and requires you to solve the problem for all the inputs to actually write the program.
Oh well
As usual, the deterministic machine has to scan the RAM to find the number, taking around 2^n steps. And as usual, the non-deterministic machine just guesses the n bits of the address in n steps and passes it to checkSolution, which jumps to the address and confirms the solution. Now, this is not an NP-complete problem in this formulation, since the contents of the RAM are not specified, so there's no mapping from other NP-complete problems to this.
Jeez, random numbers.
Given the lottery numbers for this week's lottery, compute the lottery numbers for next week's lottery. Non-deterministic machine: sure thing, done, bam. Deterministic machine: this might take a while (btw, is simulating the universe a O(n^k)-problem?) Check solution by checking bank account.
Unique inputs partial sums then. First off, sort the inputs, and treat them as a binary number where 0 is "not in solution" and 1 is "in solution".
If all the numbers in the input are such that the sum of all smaller inputs is smaller than the number, you can find the solution in linear time. For (i = input.length-1 to 0) { if (input[i] <= target) { target_bits[i] = 1; target -= input[i]; } else { target_bits[i] = 0; }}
You can prune the search space by finding a suffix that's larger than the target and by finding a prefix that's smaller than the target. Now you know that there must be at least one 0-bit in the larger suffix and at least one 1-bit in the suffix of the smaller prefix.
The time complexity of partial sums is always smaller than 2^n. For a one-bit alphabet, the time complexity is O(n). For a two-bit alphabet, the max time complexity is 2^(n/2) as you need to add two bits to the input to increment the number of elements in the input. So for an 8-bit alphabet, the max complexity would be 2^(n/8).
The complexity of partial sums approaches easy as the number of input elements approaches the size of the input alphabet. After reaching the size of the input alphabet, a solution exists if (2^a + 1) * (2^a / 2) <= target (as in, if the sum of the input alphabet is greater than or equal to target. And if the input alphabet is a dense enumeration up from 1.) You can find the solution in O(n log n): sort input, start iterating from largest & deduct from the target until the current number is larger than the target. Then jump to input[target] to get the last number. You can also do this in O(n) by first figuring out what numbers you need and then collecting them from the input with if (required_numbers[input[i]]) pick(input[i]), required_numbers can be an array of size n.
Once you reach the saturated alphabet state, you need to increase the size of the alphabet to gain complexity. So you might go from an 8-bit alphabet with a 256 element input to a 9-bit alphabet with a 256 element input (jumping from 2048 to 2304 bits in the process, hopefully boosting the complexity from O(256)-ish to O(2^256)-ish).
Thankfully, as you increase the alphabet size by a bit, your input size goes up linearly, but the saturation point of your alphabet doubles. At a fixed input size in bits, increasing the alphabet size can decrease the complexity of the problem, for each bit increase you can go from 2^(n/k) -> 2^(n/(k+1)). Likewise, by decreasing the alphabet size, you can increase the complexity of the problem. Increasing the number of elements in the input can increase the complexity of the problem, while decreasing the number of elements can decrease the complexity. The "can" is because it depends. If you're close to saturation, increasing the number of elements can nudge the problem from O(n^2) to O(n), ditto for decreasing the alphabet size. Whereas increasing the alphabet size at saturation can turn your O(n) problem into an O(2^n) problem.
As your alphabet gets larger, the discontinuities stop being so important. Anyhow, for a given partial sums input size in bits, the problem is O(n) for alphabet sizes <= log2(n). The difficulty of the problem scales with the target as well. For targets smaller than the smallest input element and for targets greater than the greatest input element, it takes O(n) time.
Tricks, hmm, the number of search-enhancing tricks you can use depends on the input. I guess the number of tricks is somehow related to the number of bits in the input and grows the program size too. The ultimate trick machine knows all the answers based on the input and has to do zero extra computation (yeah, this is the array of answers), but it's huge in size and requires you to solve the problem for all the inputs to actually write the program.
Oh well
2017-08-22
Tricks with non-determinism. Also, partial sums.
TL;DR: I've got a lot of free time.
Non-deterministic machines are funny. Did you know that you can solve any problem in O(size of the output) with a non-deterministic machine? It's simple. First, enumerate the solution space so that each possible solution can be mapped to a unique string of bits. Then, generate all bitstrings in the solution space and pick the correct solution.
Using a deterministic machine, this would run in O(size of the solution space * time to check a solution). In pseudocode, for n-bit solution space: for (i = 0 to 2^n) { if(checkSolution(i)) { return i; } } return NoSolution;
Using a non-deterministic machine, we get to cheat. Instead of iterating through the solution space, we iterate through the bits of the output, using non-determinism to pick the right bit for our solution. In pseudocode: solution = Empty; for (i = 0 to n) { solution = setBit(solution, i, 0) or solution = setBit(solution, i, 1); } if (checkSolution(solution)) { return solution; } else { return NoSolution; }
You can simulate this magical non-deterministic machine using parallelism. On every 'or'-statement, you spawn an extra worker. In the end you're running a worker on every possible solution in parallel, which is going to run in O(N + checkSolution(N))-time, where N is the number of bits in the solution.
If you're willing to do a bit more cheating, you can run it in O(checkSolution(N))-time by forgoing the for-loop and putting every solution into your 'or'-statement: solution = 0 or solution = 1 or ... or solution = 2^N; if (checkSolution(solution)) { return solution; } else { return NoSolution; }. If you apply the sleight-of-hand that writing out the solution as input to checkSolution takes only one step, this'll run in checkSolution(N). If you insist that passing the solution bits to checkSolution takes N steps, then you're stuck at O(N + checkSolution(N)).
A deterministic machine could cheat as well. Suppose that your program has been specially designed for a single input and to solve the problem for that input it just has to write out the solution bits and pass them to checkSolution. This would also run in N + checkSolution(N) time. But suppose you have two different inputs with different solutions? Now you're going to need a conditional jump: if the input is A, write out the solution to A, otherwise jump to write the solution to B. If you say that processing this conditional is going to take time, then the deterministic machine is going to take more time than the non-deterministic one if it needs to solve more than one problem.
What if you want the deterministic machine to solve several different problems? You could cheat a bit more and program each different input and its solution into the machine. When you're faced with a problem, you treat its bitstring representation as an index to the array of solutions. Now you can solve any of the problems you've encoded into the program in linear time, at the expense of requiring a program that covers the entire input space. (Well, linear time if you consider jumps to take constant time. If your jumps are linear in time to their distance... say you've got a program of size 2^N and a flat distribution of jump targets over the program. The jumps required to arrive at an answer would take 2^(N-1) time on average.)
Note that the program-as-an-array-of-solutions approach has a maximum length of input that it knows about. If you increase the size of your input, you're going to need a new program.
How much of the solution space does a deterministic machine need to check to find a solution? If we have a "guess a number"-problem, where there's only one point in the solution space that is the solution, you might assume that we do need to iterate over the entire space to find it in the worst case. And that would be true if checkSolution didn't contain any information about the solution. In the "guess a number"-problem though, checkSolution contains the entire answer, and you can solve the problem by reading the source to checkSolution.
Even in a problem like partial sums (given a bunch of numbers, does any subset of them sum to zero; or put otherwise: given a bunch of positive numbers, does any combination sum to a given target number), the structure of the problem narrows down the solution space first from n^Inf to n! (can't pick the same number twice), then to 2^n (ordering doesn't matter) and then further to 2^n-n-1 (an answer needs to pick at least two elements), and perhaps even further, e.g. if the first number you pick is even, you can narrow down its solution subtree to combinations of even numbers and pairs of odd numbers. Each number in the input gives you some information based on the structure of the problem.
The big question is how fast the information gain grows with the size of the input. That is, suppose your input size is n and the solution space size is 2^n. If you gain (n-k) bits of solution from the input, you've narrowed the solution space down to 2^(n-(n-k)) = 2^k. If you gain n/2 bits, your solution space becomes 2^(n/2). What you need to gain is a magical number that plonks exp(f(n)) <= k n^(k-1). If there is such an f(n), you can find a solution to your problem in polynomial time.
If your input and checkSolution are black boxes, you can say that a deterministic machine needs to iterate the entire solution space. If checkSolution is a black box, you can do the "guess a number"-problem. If your input is also a black box, you can't use partial solutions to narrow down the solution space. For example, in the partial sums problem, if you only know that you've picked the first and the seventh number, but you don't know anything about them, you can only know if you have a solution by running checkSolution on your picks. If you can't get any extra information out of checkSolution either, you're stuck generating 2^n solutions to find a match.
How about attacking the solution space of partial sums. Is the entire solution space strictly necessary? Could we do away with parts of it? You've got 2^n-n-1 different partial sums in your solution space. Do we need them all? Maybe you've got a sequence like [1,2,-3,6], that's got some redundancy: 1+2 = 3 and -3+6 = 3, so we've got 3 represented twice. So we wouldn't have to fill in the entire solution space and could get away with generating only parts of it for any given input? Not so fast. Suppose you construct an input where every entry is double the size of the previous one: e.g. [1,2,4,8,16, ...]. Now there are 2^n-1 unique partial sums, as the entries each encode a different bit and the partial sums end up being the numbers from 1 to 2^n-1.
But hey, that sequence of positive numbers is never going to add up to zero, and the first negative number smaller than 2^n is going to create an easy solution, as we can sort the input and pick the bits we need to match the negative number. Right. How about [1, -2, 4, -8, 16, -32, ...]? That sequence generates partial sums that constitute all positive numbers and all negative numbers, but there is no partial sum that adds up to zero, and no partial sum is repeated. If your algorithm is given a sequence like this and it doesn't detect it, it'll see a pretty dense partial sum space of unique numbers that can potentially add up to zero. And each added number in the input doubles the size of the partial sum space.
Can you detect these kinds of sequences? Sort the numbers by their absolute value and look for a sequence where the magnitude at least doubles after each step. Right. What if you use a higher magnitude step than doubling and insert one less-than-double number into the sequence in a way such that the new number doesn't sum up to zero with anything? You'll still have 2^n unique partial sums, but now the program needs to detect another trick to avoid having to search the entire solution space.
If the input starts with the length of the input, the non-deterministic machine can ignore the rest of the input and start generating its solutions right away (its solutions are bitstrings where e.g. for partial sums a 1 means "use this input in the sum" and a 0 means "skip this input"). The deterministic machine has to read in the input to process it. If the input elements grow in size exponentially, the deterministic machine would take exponentially longer time to read each input. Suppose further that the possible solution to the problem consists of single digit numbers separated by exponentially large inputs and that jumping to a given input takes a constant amount of time (this is the iffy bit). Now the non-deterministic machine still generates solutions in linear time, and checkSolution only has to deal with small numbers that can be read in quickly, but the deterministic machine is stuck slogging through exponentially growing inputs.
You might construct a magical deterministic machine that knows where the small numbers are, and can jump to consider only those in its solution. But if you want to use it on multiple different inputs, you need to do something different. How about reading the inputs one bit at a time and trying to solve the problem using the inputs that have finished reading. Now you'll get the small numbers read in quickly, find the solution, and finish without having to consider the huge inputs.
If the solution uses one of the huge inputs, checkSolution would have to read it in and become exponential. Or would it? Let's make a padded version of the partial sums problem, where the input is an array of numbers, each consisting of input length in bits, payload length in bits, and the payload number padded with a variable-size prefix and suffix of zeroes and a 1 on each end, e.g. you could have {16, 3, 0000 0101 1100 0000} to encode 011. The checkSolution here would take the index of the number in the input array and size of its prefix. This way checkSolution can extract and verify the padded number with a single jump.
Now, the deterministic machine would have to search through the input to find a one-bit, using which it could then extract the actual number encoded in the input. For exponentially growing inputs, this would take exponential time. The non-deterministic machine can find the input limits quickly: for (i = 0 to ceil(log2(input_bitlength))) { index_bits[i] |= 1 or 0 }. The non-deterministic machine can then pass the generated indices alongside with the generated partial sum permutation to checkSolution, which can verify the answer by extracting the numbers at the given indices and doing the partial sum.
Approaching it from the other direction, we can make a program that generates an exponential-size output for a given input. Let's say the problem is "given two numbers A and B, print out a string of length 2^(2^A), followed by the number B." Now (if jumps are constant time), checkSolution can check the solution by jumping ahead 2^(2^A) elements in the output, reading the rest and comparing with B. You can imagine a non-deterministic machine with infinite 'or'-statements to generate all strings (which by definition includes all strings of length 2^(2^A) followed by the number B.) The problem is that if writing any number of elements to checkSolution is free, the deterministic machine could also check A, execute a single command to write 2^(2^A) zeroes to checkSolution and another to append the number B. If there is no free "write N zeroes"-loophole in the machine, and it must generate the string of zeroes by concatenating strings (let's say concatenating two strings takes 1 step of time), we've got a different case. Start off with a string of length 1, concatenate it with itself and you have 2, repeat for 4, etc. To get to a string of length 2^(2^A), you need to do this 2^A times.
But hey, doesn't checkSolution have to generate the number 2^(2^A) too to jump to it? And doesn't that take 2^A time? You could pass it that, sure, but how can it trust it? If checkSolution knows the length of its input (through some magic), it could jump to the end of it and then the length of B backwards. But it still needs to check that the length of its input is 2^(2^A) + length(B). If you were to use 2^A instead of 2^(2^A), you could make this work if string creation needs one time step per bit. (And again, if passing a solution to checkSolution takes no time.)
So maybe you set some limits. The machines need to be polynomial in size to input, and they need to have a polynomial number of 'or'-statements. Jumps cost one time step per bit. Passing information to checkSolution takes time linear to the length of the info. You have access to checkSolution and can use it to write your machine. Each machine needs to read in the input before it can start generating a solution.
What's the intuition? Partial sums takes an input of size n and expands it to a solution space of 2^n, and the question is if you can compress that down to a solution space of size n^k (where n^k < 2^n for some n). A naive enumeration of the solution space extracts 0 bits of solution information from the input, hence takes 2^n steps but is small in size. A fully informed program can extract full solution information from the input (since the input is basically an array index to an array of answers), but requires storing the entire 2^n solution space in the program. Is there a compression algorithm that crunches the 2^n solution space down to n^k size and extracts a solution in n^m steps?
Partial sums is a bit funny. For fixed-size input elements that are x bits long, and a restriction that the input can't have an element multiple times, partial sums approaches linear time as the number of input elements approaches 2^x. If the input contains every different x-bit number, it can generate all the numbers up to the sum of its input elements (i.e. the input defines a full coverage over the codomain). In fact, if the input contains every one-bit number up to n bits, you can generate every number n bits long.
The time complexity of unique set partial sums starts from O(n) at n=1 and ends up at O(n) at n=2^n. (Or rather, the time complexity is O(n) when n equals the size of the input alphabet.) It feels like the complexity of partial sums on a given alphabet is a function that starts from O(n) and ends at O(n) and has up to O(2^n) in the middle.) There's an additional bunch of O(n) solutions available for cases where the input includes all one-bit numbers up to 2^ceil(log2(target)). And a bunch of O(n log n) solutions for cases where there's a 2-element sum that hits target (keep hashtable of numbers in input, see if it contains target - input[i]). And for the cases where there are disjoint two-element sums that generate all the one-bit numbers for the target.
The partial sums generated by an input have some structure that can be used to speed up the solution in a general case. If you sum up all the numbers in the input, you generate the maximum sum. Now you can remove elements from the max sum to search for the target number from above and below. With the two-directional search, the difficult target region becomes partial sums that include half of the input elements. There are n choose n/2 half sums for an input of size n. The derivative of n choose n/2 approaches 2 as n increases, doubling the number of half sums on each step in input size.
You can also start searching from the target number. Add numbers to the target and try to reach max sum and you know which numbers you need to subtract from max sum to make up the target. Subtract numbers from the target and try to reach one of the inputs to find the numbers that make up the target.
Combining the two approaches. If you think of this thing as a binary number with one bit for each input element, on/off based on whether the element is in the solution. The bottom search runs from all zeroes, turning on bits. The max sum search runs from all ones, turning bits off. The from-target searches run from all zeroes and all ones, turning bits on or off respectively.
There is an approach for rejecting portions of the search space because they sum to a number higher than the target. Sort the input by magnitude, sum up the high end until the sum is larger than the target. Now you can reject the portion of the search space with that many top bits set. As the attacker, you want to craft a target and an input such that the search algorithm can reject as little of the search space as possible, up to the half sums region. However, this creates a denser enumeration in the half sums region, which makes clever search strategies more effective (e.g. suppose you have numbers from 1 to 4: now you know that you can create any number up to 10 out of them.)
To make the input hard, you should make the target higher than the largest number in the input, but small enough that it doesn't require the largest number in the input, the target should require half of the input elements, the input elements should avoid dense enumerations, one-bit numbers, partial sums that add up to one-bit numbers, disjoint bit patterns (and disjoint complements), the number of input elements should be small compared to the input alphabet, and they should be widely distributed while remaining close to target / n (hah). Your inputs should probably be co-prime too. And you should do this all in a way that doesn't narrow the search space to "the top hardest way to build the target number out of these inputs".
For repeated number partial sums, if your input alphabet size is two, it runs in O(n), as the partial sums of zeroes and ones is a dense enumeration up to the number of ones in your input. For other repeated sums, it's difficult. Maybe you could think of them as modulo groups. And somehow make them work like uniques time-complexity-wise.
The trouble in partial sums are carries. If you change the problem to "does the binary OR of a subset of the input elements equal the target", the problem becomes easier "for all bits in the target, find an input that has that bit and none of the bits in the target's complement", which turns into target_check_bits[i] |= input[x][i] & !(input[x] & !target).
Once you throw in the carries, suddenly there are multiple ways to produce any given bit. If you know that there are no carries in the input (that is, each bit appears only once in the input), the problem turns into the binary OR problem.
2017-08-04
Acceleration, 3
Oh right, right, I was working on this. Or something like this. Technology research post again :(
First I was working on this JavaScript ray tracer with BVH acceleration and voxel grid acceleration. And managed to get a 870k dragon loaded into it and rendered in less than 30 seconds... In quite unoptimized single-threaded JavaScript.

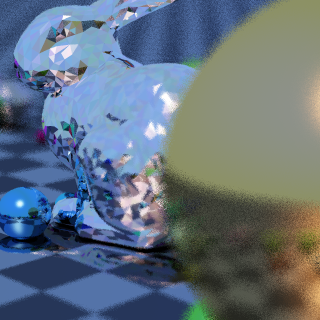




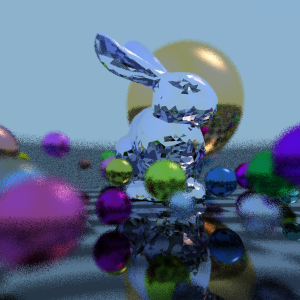

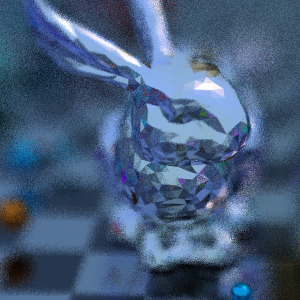


Then I had an idea and spent two weeks doing noise-free single-sample bidirectional path tracing. But it turns the high-frequency noise into low-frequency noise and runs too slow for realtime. I'll have to experiment more with the idea. Shadertoy here. Start with the writeup and screenshots after that.



















First I was working on this JavaScript ray tracer with BVH acceleration and voxel grid acceleration. And managed to get a 870k dragon loaded into it and rendered in less than 30 seconds... In quite unoptimized single-threaded JavaScript.

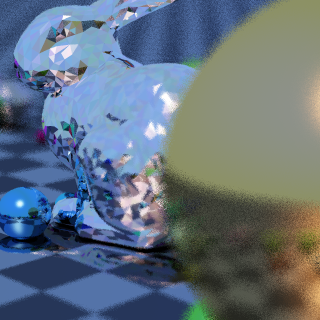




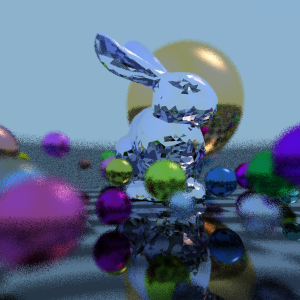

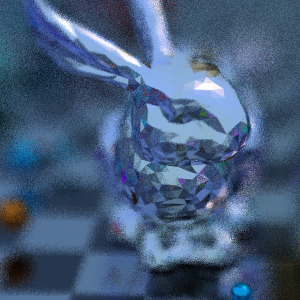


Then I had an idea and spent two weeks doing noise-free single-sample bidirectional path tracing. But it turns the high-frequency noise into low-frequency noise and runs too slow for realtime. I'll have to experiment more with the idea. Shadertoy here. Start with the writeup and screenshots after that.
Single-sample bidirectional path tracing + hemisphere approximation
Smooth indirect illumination by creating the incoming light hemisphere on the fly
based on the hemisphere samples of the surrounding pixels.
See also: Virtual point lights, bidirectional instant radiosity
First pass: Create path suffixes = point with incoming ray of light.
1. Shoot out primary ray and bounce it off the hit surface.
2. Trace the first bounce and store its hit point, normal and material.
3. Trace the rest of the path from the first bounce point and store the direction of the path.
4. Store the amount of light at the first bounce point.
Now you have a path suffix at each pixel that has enough info to connect any other path to it.
Second pass: Connect the primary ray to path suffixes in surrounding pixels.
1. Shoot out primary ray and calculate direct light for it
2. Sample NxN samples around the pixel from the path suffix buffer
3. Accumulate the light from the hemisphere. For each sample:
3.1. Calculate the direction to it: hd = normalize(sample.p - primary.p)
3.2. Accumulate light according to the BRDFs of the primary point and the hemisphere point.
[3.3. Scale the light contribution with a pixel distance filter for smoother transitions]
Extra passes: Create new path suffixes by connecting points in path suffix buffer to other path suffixes
1. Primary ray hits can act as path suffixes for hemisphere points (and have nice geometric connection at same px coord).
2. Hemisphere points can act as path suffixes for hemisphere points (but may lie on the same plane near px coord).
3. Add light from new path suffixes to primary hits.
Why this might be nice?
- Get more mileage from paths: in scenes with difficult lighting conditions, the chances of
finding light are low for any given path. By summing up the contributions of 10000 paths,
you've got a much higher chance of finding light for a pixel.
- Less noise: noise is variance in hemisphere sampling. If neighbouring pixels have similar
hemispheres, there's smooth variance and little noise.
- If you have the budget, you can cast shadow rays to each hemisphere point and get correct lighting.
- If you don't have the budget, you can use the hemi points as soft light and get blurry lighting
- You can use the found hemisphere light to approximate a point's light distribution and guide your sampler.
- You can use light samples from previous frames.
What sucks?
- If you don't cast shadow rays, you get light bleeding and everything's blurry.
- Casting 1000 shadow rays per pixel is going to have an impact on performance
- Direct lighting remains noisy
(you can use direct light as a hemisphere sample but it causes even more light bleeding w/o shadow rays)
- This scene smooths out at 64x64 hemisphere samples per pixel, which is expensive to sample
- Increasing the size of your sampling kernel increases inaccuracies w/o shadow rays
- It seems like you trade high-frequency noise for low-frequency noise
- Glossy stuff is hard
The ugly:
- Using three buffers to trace because no MRTs, otherwise could store hemi hit, normal, dir, primary hit,
hemi color, primary color on a single trace, and recombine on the second pass.
- Slow SDF ray marcher as the rendering engine
- Not storing incoming light dir atm, all the lighting equations are hacks in this demo



















Subscribe to:
Posts (Atom)