I'd like to draw a tree, but how? Let's start by writing a simple draw loop:
module Main where
import Graphics.Rendering.Cairo
import Canvas
main = canvas draw 600 600
draw w h t = do
color white
rectangle 0 0 w h
fill
color black
drawTree w h t
Then, what is a tree? A tree is sort of a recursive forking function. A
scanl towards the sun. Every year its branches grow in thickness, possibly forking.
Let's define a simple branch as a function of age and angle. A branch of age 0 has no forks. A branch of age N has 2 sub-branches of age N-1.
branch 0 angle = [map (rotateP angle) [(0,0), (0, -1)]]
branch n angle =
this ++ subBranches
where
this = branch 0 angle
[[_,(x,y)]] = this
subBranches = map (map (translateP x y)) (left ++ right)
left = branch (n-1) (angle-pi/8)
right = branch (n-1) (angle+pi/8)
To draw the branches, we need to write the drawTree procedure. Here's one that draws a tree of age 7 and rotates it in the middle of the screen:
drawTree w h t = do
translate (w/2) (h/2)
rotate t
mapM_ strokeLine tree
where tree = map (map (uscaleP 25)) $ branch 7 0
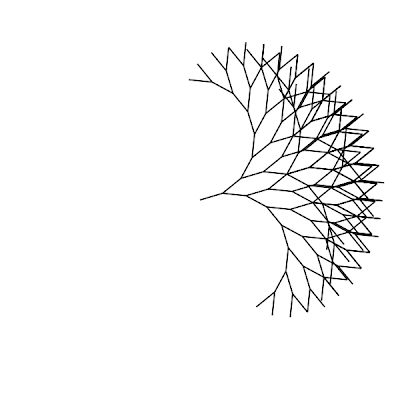
You can see the result on the right. Not the prettiest tree in the land. Let's make the branches get thicker with age.
To draw lines of different thickness, we need to add the thickness information to the line data structure. Previously it was a list of (x,y)-tuples, with width it becomes a (lineWidth, (x,y) list)-tuple. A couple combinators will help here:
strokeWidthLine = tupleDo lineWidth strokeLine
mapWidthLine f = fupleR (map f)
fupleR f (a,b) = (a, f b)
Then rewrite branch and drawTree to use width-carrying lines:
drawTree w h t = do
translate (w/2) h
mapM_ strokeWidthLine tree
where tree = map (mapWidthLine (uscaleP 25)) $ branch 8 0
branch 0 angle = []
branch n angle =
(thickness, points) : subBranches
where
points = map (rotateP angle) [(0,0), (0, -1)]
thickness = n
[_,(x,y)] = points
subBranches = map (mapWidthLine (translateP x y)) (left ++ right)
left = branch (n-1) (angle-pi/8)
right = branch (n-1) (angle+pi/8)

Now the tree grows from the bottom of the screen and looks a bit more aesthetically pleasing. Next we could make the branches rotate and grow with an upwards bias. Compute distance from up-vector and scale points and the angle accordingly. Something like this:
da = angularDistance 0 angle
scale = 3 * ((1-(abs da / pi)) ** 2)
points = map (rotateP (angle + da/3) . uscaleP scale) [(0,0), (0, -1)]
And then, hmm, random angles for the branches? That needs a bit of extra work. The random number generator is in the IO monad, whereas
draw is in the Render monad, and
branch is a pure function. So, extend
main to get a pure list of random Doubles, then pass that to
draw, which passes it to
drawTree and
branch.
main = do
gen <- getStdGen
let ns = randoms gen :: [Double]
canvas (draw ns) 600 600
draw ns w h t = do
color white
rectangle 0 0 w h
fill
color black
drawTree ns w h t
drawTree ns w h t = do
translate (w/2) (h+5)
mapM_ strokeWidthLine tree
where tree = map (mapWidthLine (uscaleP 25)) $ branch ns 8 (pi/2*sin t)
And make branch do something with it:
branch _ 0 _ = []
branch (r1:r2:rs) n angle =
[...snip...]
left = branch (takeOdd rs) (n-1) (angle - r1*pi/4)
right = branch (takeEven rs) (n-1) (angle + r2*pi/4)
takeOdd [] = []
takeOdd [x] = []
takeOdd (_:x:xs) = x : (takeOdd xs)
takeEven [] = []
takeEven [x] = [x]
takeEven (x:_:xs) = x : (takeEven xs)
The result of all this tomfoolery is a tree that looks a bit more natural than the geometric trees above.

The trees at the top of this post use random numbers for scaling the branches as well, so they're even more noisy.
Here's the source code:
tree.hs and
canvas.hs.
Compile by doing
ghc --make tree.hs canvas.hs -o tree