The four faces on the left are made up of Hanzi/Kanji radicals, the middle face is hiragana, the left-side faces are Hangeul, Latin, and Greek. The face left of the bunny and the bunny itself are Cyrillic.
One thing that's been interesting me during the writing system study is how writing systems affect the drawings of the people who use them. I mean, if you're going to draw something, you're going to use the strokes and patterns you already know. And the patterns you know best are the ones you use every day, so the writing system should have a impact on the drawings. There seems to be a feedback effect at work here: the things you draw turn into writing and the writing guides your drawing.
To explain, drawing and writing are both ways to communicate information visually. The old writing systems were in fact formalized alphabets of simplified drawings (or not so simplified drawings in the case of Egyptian hieroglyphs). And these drawings were based on the surrounding nature of the time the writing system was made, hence you have cobras, pintail ducks, flamingos, jackals, crocodiles and hippos in the hieroglyphs. Had it been a Northern European writing system, it would've had wolves, elks and bears instead of the Nile fauna.
One example of writing systems affecting drawing that's easy to reason about are emoticons. You mostly do emoticons that are easy to type and don't get mangled in the transmission. With a Latin keyboard layout you get emoticons with Latin characters and punctuation. With a Korean keyboard, you get Korean emoticons. There's a feedback effect here as well: emoticons create an alphabet of emotions, that you then use in your drawings as a shorthand for the emotions in question. And when you draw an emotion without an emoticon, someone might figure out a way to simplify that drawing into an emoticon, which is then added to the alphabet and used by people drawing emotions...
And then you have writing systems designed for drawing. Perhaps I could segue from drawing writing systems to learning circuit analysis.
To take this drawing with writing thing further, Islamic calligraphy is one famous example:

Image courtesy of Wikipedia.
And the Egyptian Book of the Dead... those big guys there are more like 180pt calligraphy than drawings. Even their sculptures veer towards being big 3D letters carved from stone.
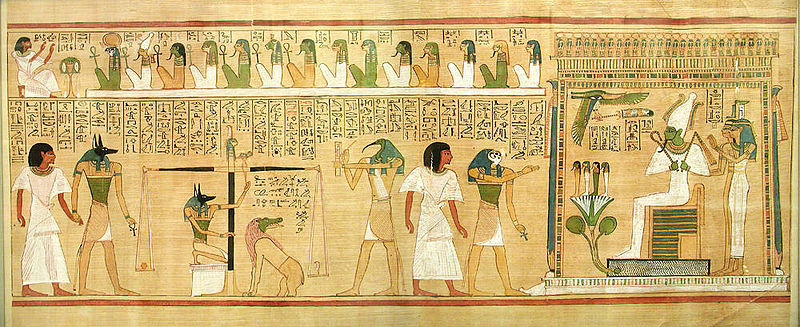

Images courtesy of Wikipedia. Click to see the pages.